Joint Models of Disagreement and Stance
This post accompanies the PSL model and corpora described in the “Joint Models of Disagreement and Stance” ACL paper.
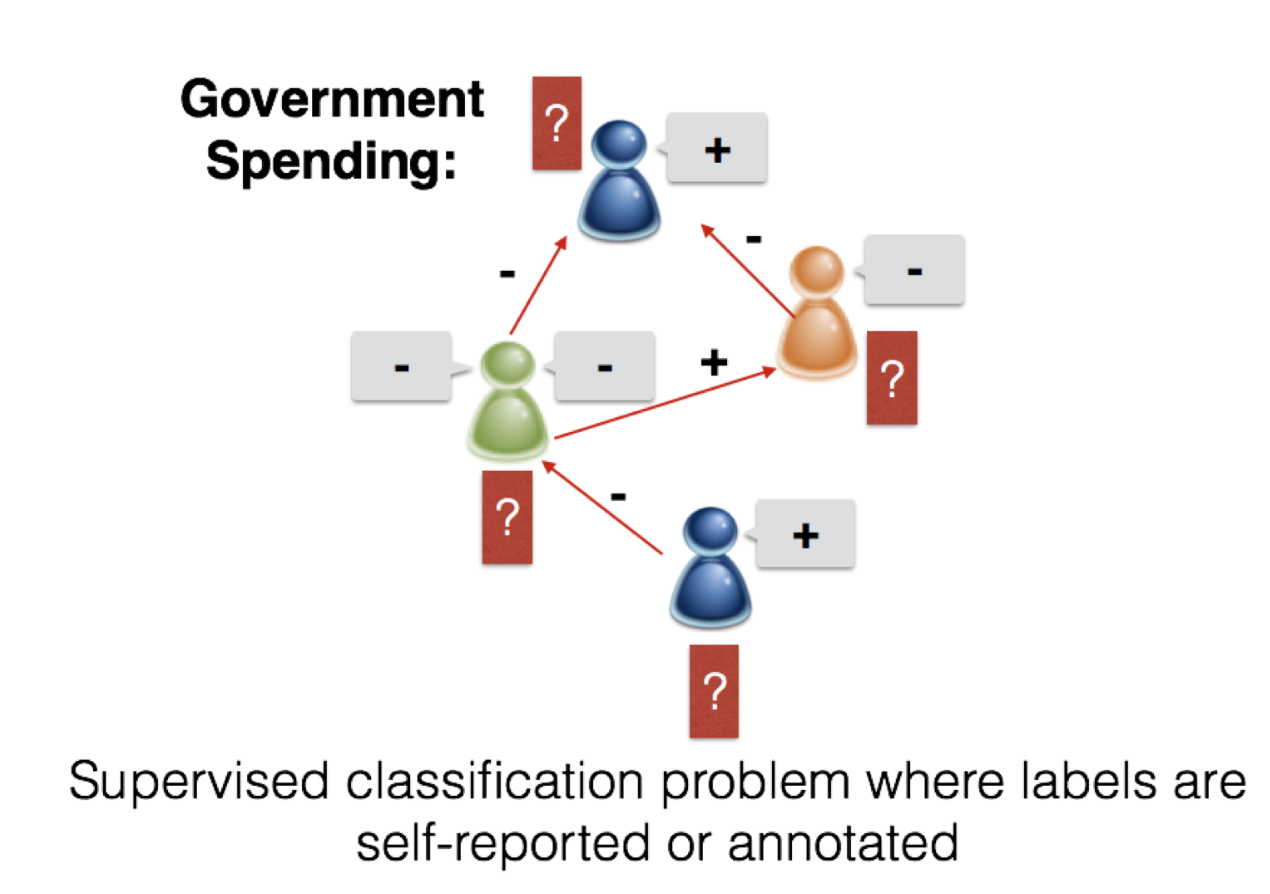
In this PSL inference task, we’ll work with text from online debate forums. An online debate forum, e.g. createdebate.org, features debates on several socio-political issues, or topics. For example, one topic might be whether or not the government should increase spending, which we’ll succinctly call “spending.” A user starts a debate by writing a post in which she indicates her stance towards the topic. For simplicity throughout, we’ll consider pro and anti as the stances. Let’s suppose she’s pro-spending. Another user replies to this user to argue his opposing point, and his post will contain language indicating his anti-spending view and textual cues that he disagrees with our original user.
We can view these exchanges on an online debate site as a complex graph with vertices and edges. We have both user and post vertices, connected by a type of directed edge that tells us which user wrote which post. Of course, the post is associated with its text, which we can describe as an array of unigrams appearing in that post. We also have directed edges connecting users when one user replies to another.
When we want to build machine learning models, we also associate random variables of interest to either these nodes (users, posts) or edges (replies) whose values we want to infer. In this example, we will jointly predict the stances of all users and whether or not replying users disagree or agree on stance. Each user will have a binary pro/anti stance variable which we will build a model to infer. Each reply edge will also be associated with a binary same/opposite stance variable which our model will predict together with stance.
Let’s see the step-by-step approach to building this PSL model using predicates and rules:
First, we’ll specify predicates for our target random variables – stance and disagreement. We represent stance of a user with:
isPro(User, Topic)
Where variable U will be substituted all the users in our dataset and variable T will substituted with all topics in our domain.
As an example, if we had just one topic, “spending” and two users, “alice” and “bob”, we will get the following ‘ground atoms’ of isPro(User, Topic):
isPro("alice", "spending")
isPro("bob", "spending")
Remember that we want to predict the values for these atoms and in PSL, we infer values between 0 and 1. For example, if “alice” uses pro-spending language and “bob” uses anti-spending language, we’d like to infer values like:
isPro("alice", "spending") = 0.9
isPro("bob", "spending") = 0.1
Next, we need a way of using the language in users’ posts as a signal to our model. In this problem, we train a logistic regression classifier outside of PSL whose features are counts of unigrams from all of a users’ posts and whose training data are pro/anti labels for all users. However, this classifier uses only information “local” to each user and can easily make mistakes since language is ambiguous. We encode this signal with the predicate:
localPro(User, Topic)
We observe the class probabilities from our logistic regression classifier as its values. For example, our noisy local classifier might output, for “alice” and “bob”
localPro("alice", "spending") = 0.4
localPro("bob", "spending") = 0.6
To use PSL to smoothen these errors, let’s make use of our insight that the text also signals same/opposite stance notions of disagreement between users who reply to one another. Exactly like stance, we can specify a disagreement random variable to infer:
disagrees(User1, User2)
Where User1 replies to User2 in a thread, and our training label for this prediction is 1 if User1 and User2 have the same stance and 0 otherwise.
We similarly train a local logistic regression classifier based on unigrams and encode that signal similarly to stance:
localDisagree(User1, User2)
Suppose that for “alice” and “bob”, we have a stronger disagreement signal based on the words “bob” uses to debate with “alice”. We might observe the following local prediction for disagreement:
localDisagree("alice", "bob") = 0.8
This information should help us make better stance inferences! How can we model these two prediction problems with PSL rules?
Let’s start by using our local logistic regression text classifiers to inform our final stance and disagreement predictions with the rules:
localPro(U, T) >> isProAuth(U, T)
~localPro(U, T) >> ~isProAuth(U, T)
localDisagrees(U1, U2) >> disagrees(U1, U2)
~localDisagrees(U1, U2) >> ~disagrees(U1, U2)
We see that rules such as the second rule allow us to also reason about when a user’s stance is not pro by using the class probability of anti from our logistic regression classifier. Now, let’s see how disagreement can help us predict users’ stances:
disagrees(U1, U2) & responds(U1, U2) & participates(U2, T) &
isProAuth(U1, T) >> ~isProAuth(U2, T)
disagrees(U1, U2) & responds(U1, U2) & participates(U1, T) &
participates(U2, T) & ~isProAuth(U1, T) >> isProAuth(U2, T)
We don’t need to worry about auxiliary predicates like responds and participates. They simply give us information about who replied to whom and whether users participate in a certain topic T. When PSL grounds these rules, these predicates help define the population of constants that should be involved in the ground rules.
For ease, let’s consider the logic that’s doing the work in this rule:
disagrees(U1, U2) & isProAuth(U1, T) >> ~isProAuth(U2, T)
disagrees(U1, U2) & ~isProAuth(U1, T) >> isProAuth(U2, T)
These two rules encode our intuition that if two users likely disagree, they should have opposite stances. We have two rules to encode both combinations of possible stance assignments to the users. Importantly, these rules help us make collective inferences, where the predicted stance of one user depends on that of a neighboring user in the debate graph. We can easily detect collective rules by recognizing that a target predicate is in both the body and head of the rule.
Now, we’ll want to encode a similar intuition for agreement: if users probably agree, they should the same stance. Again, for ease, let’s see the core logic that does all the inference legwork:
~disagrees(U1, U2) & ~isProAuth(U1, T) >> ~isProAuth(U2, T)
~disagrees(U1, U2) & isProAuth(U1, T) >> isProAuth(U2, T)
But we want to similarly use stance variables to inform disagreement and agreement. We can encode the same intuitions as above with the following logic:
isProAuth(U1, T) & ~isProAuth(U2, T) >> disagrees(U1, U2)
~isProAuth(U1, T) & isProAuth(U2, T) >> disagrees(U1, U2)
~isProAuth(U1, T) & ~isProAuth(U2, T) >> ~disagrees(U1, U2)
isProAuth(U1, T) & isProAuth(U2, T) >> ~disagrees(U1, U2)
Notice that in these rules, stance variables are in the body of the rule and disagreement is in the head. Let’s turn back our example where we observed:
localPro("alice", "spending") = 0.4
localPro("bob", "spending") = 0.6
localDisagree("alice", "bob") = 0.8
With the rules above, we can expect to see that the final inferences for isPro("alice", "spending") and isPro("bob", "spending") will be sided correctly unlike the local stance predictions because the local disagreement signal combined with the collective rules will propagate correct information.
Now that we’ve looked at the predicates and rules of our joint disagreement and stance PSL model, let’s run inference on a real debate topic and set of discussions.
Download the code and data by cloning this git repository: https://bitbucket.org/linqs/psl-joint-stance.git.
Let’s go to psl-forums directory.
Before running a simple example, navigate to data/simple_abortion/0/train and familiarize yourself with the input files for the predicates described above.
You’ll see a corresponding .csv file for each predicate name.
Remember that while we observe values for: localPro, localDisagree, participates, responds.
The files for disagrees and isProAuth tell us who the users (or authors) are that we have training labels for (or in the case of the test set, ground truth labels) and gives us training labels so that we learn weights for each rule.
Navigate back to the psl-forums directory and use ./run_simple.sh to run cross validation on a single forum topic.
There are 5 train/test splits and the code learns weights using the stance and disagreement labels in train and evaluates the inferred values for targets in the test directory.
When complete, the output should show:
[main] WARN edu.ucsc.cs.JointStanceDisagreementPrediction - Accuracy: 0.7203389830508474
[main] WARN edu.ucsc.cs.JointStanceDisagreementPrediction - Accuracy: 0.6233766233766234
[main] WARN edu.ucsc.cs.JointStanceDisagreementPrediction - Accuracy: 0.676056338028169
[main] WARN edu.ucsc.cs.JointStanceDisagreementPrediction - Accuracy: 0.6466165413533834
[main] WARN edu.ucsc.cs.JointStanceDisagreementPrediction - Accuracy: 0.6509433962264151
This gives us the accuracy of prediction on the test set for each random split. You can experiment by commenting out combinations of rules and evaluating the accuracy.
You can also run the full set of cross-validation experiments described in our paper.
To do this, first run ./fetch_data.sh in the data directory.
Then from the psl-forums directory, call ./run_full_experiment.sh.