Hybrid Recommender Systems Using PSL
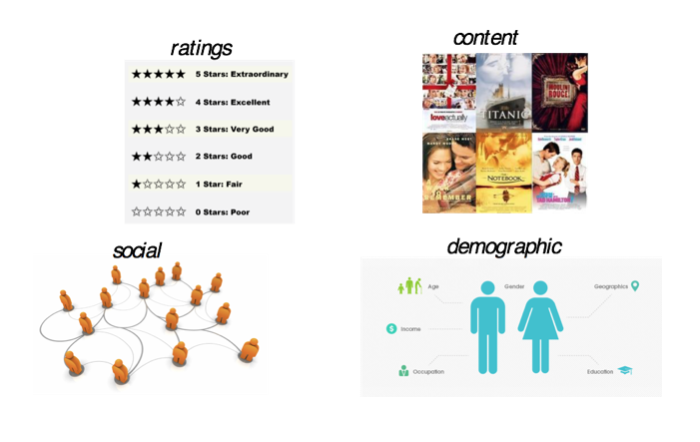
In traditional recommender systems, recommendations are usually made by using the information provided by a rating matrix. However, new recommender systems have access to much richer information. For example, in a movie recommender system information about the content of the movies might be available, like actors, directors, plot, etc. Additionally, there might be social information available for the users, e.g., a user might login to the recommender system through his Facebook account. More than that, demographic information about the user might be available, such as age or gender. In this post we will show that all this rich information can be used to improve recommendations by using PSL.
The related work has shown that combining rating information with other data sources improves recommendation performance. Early work on the field combines ratings with information about the content of the items and improves performance. This is easily explainable: if a user likes one horror movie, it’s probable that she will like other horror movies as well. Moreover, as social media became popular, relationship information is also found to be useful in the recommender system setting. This is easily explainable again: homophily states that we are connected with people who are similar to us, so we may share the same tastes with our friends.
Finally, ensemble methods, which combine the predictions of multiple recommender algorithms, are also known to improve performance. This was one of the biggest lessons learned from the Netflix competition, that “predictive accuracy is substantially improved when blending multiple predictors” [Bell et al.].
Related work has proposed hybrid recommender systems that have been shown to work better than non-hybrid systems. However, these systems typically fall short on at least one of our desirata: generality, extensibility, or scalability. Most of the work so far combine collaborative filtering with only simple content features, or just one other data modality. On the other hand, probabilistic graphical modeling approaches proposed for recommendations are typically more general than other hybrid models. However, they suffer in terms of scalability when it comes to practical real-world recommendation tasks. These models are expected to be computationally challenging in the general case, as Inference is NP-hard.
To address this challenge, we propose to use PSL to build a hybrid framework which we call HyPER: the hybrid probabilistic extensible recommender. Hyper is a general, extensible, and scalable recommender framework.
To build HyPER, we view the problem as a bipartite graph where users and items are nodes (Figure 2). Edges illustrate ratings of users over items. The weights on the edges represent the value of the rating. Dashed edges represent unobserved ratings the values of which we wish to predict.
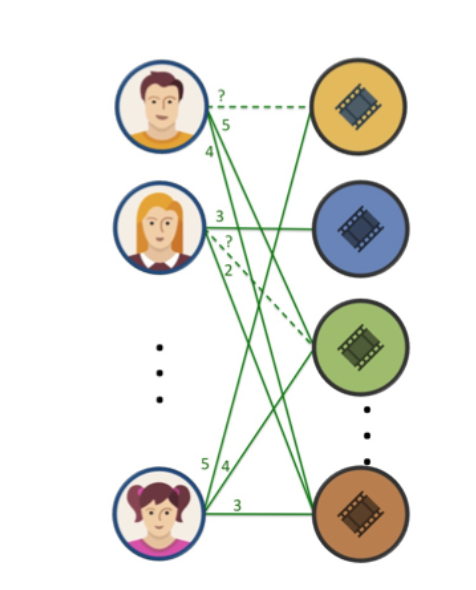Figure 2: Recommendation graph when only ratings are available
We build the hybrid model by adding edges to this graph. Additional edges represent the additional information provided by different sources. For example we can represent social relationships between users by adding edges between users. Figure 3 presents the extended recommendation graph that we produce to encode all different information sources and algorithms. More specifically, we encode user similarities that come from the user-based neighborhood methods and social information by adding edges between users. We encode item similarities that come from the item-based neighborhood methods and content information by adding between items. We finally encode predictions from other algorithms by adding edges between users and items. The missing ratings are predicted by reasoning over the enhanced graph by performing inference in a graphical model.
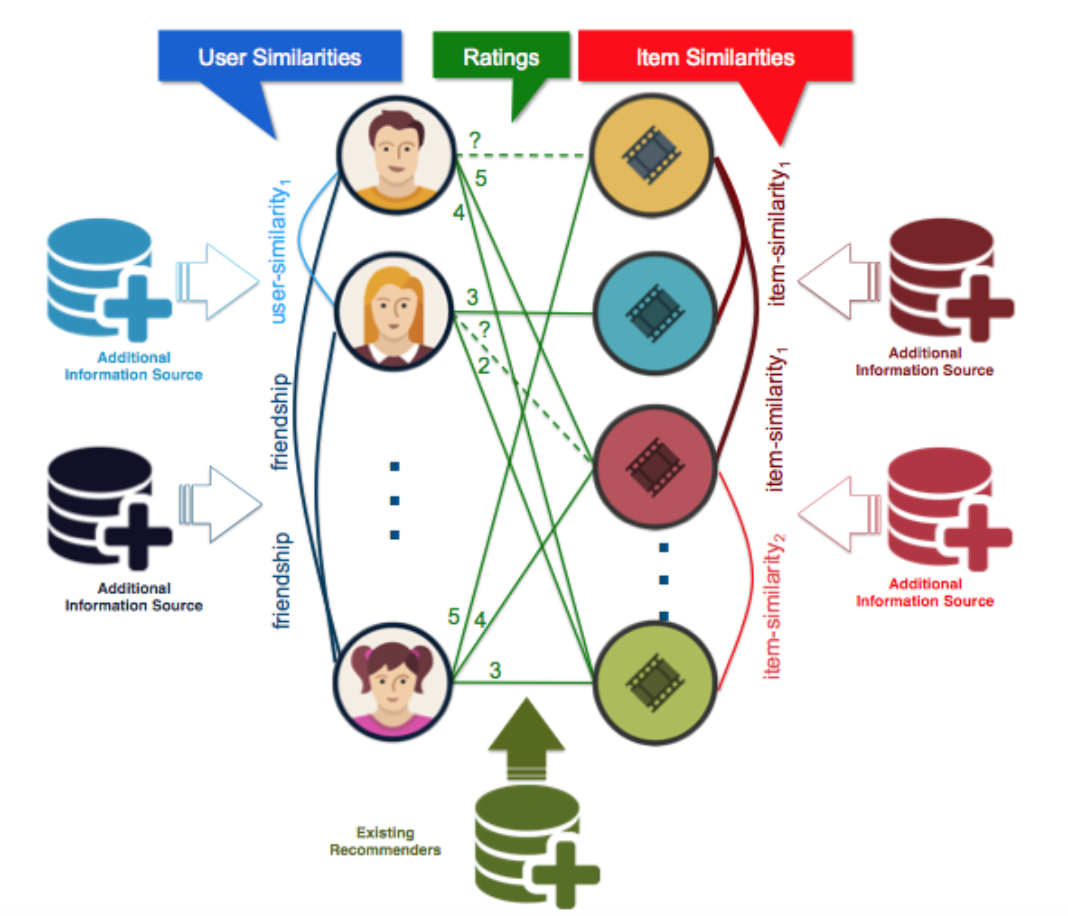Figure 3: Recommendation graph when additional information (e.g., user and item similarities) are available.
After defining the recommendation graph, we need to reason over it to make predictions. As initially discussed, we use PSL because the formalism of this model allows exact, efficient, and scalable inference. In particular, we use first order PSL logical rules to define our hybrid recommender model. First, we introduce rules from item-based neighborhood methods. The intuition is that similar items get similar ratings by a given user.
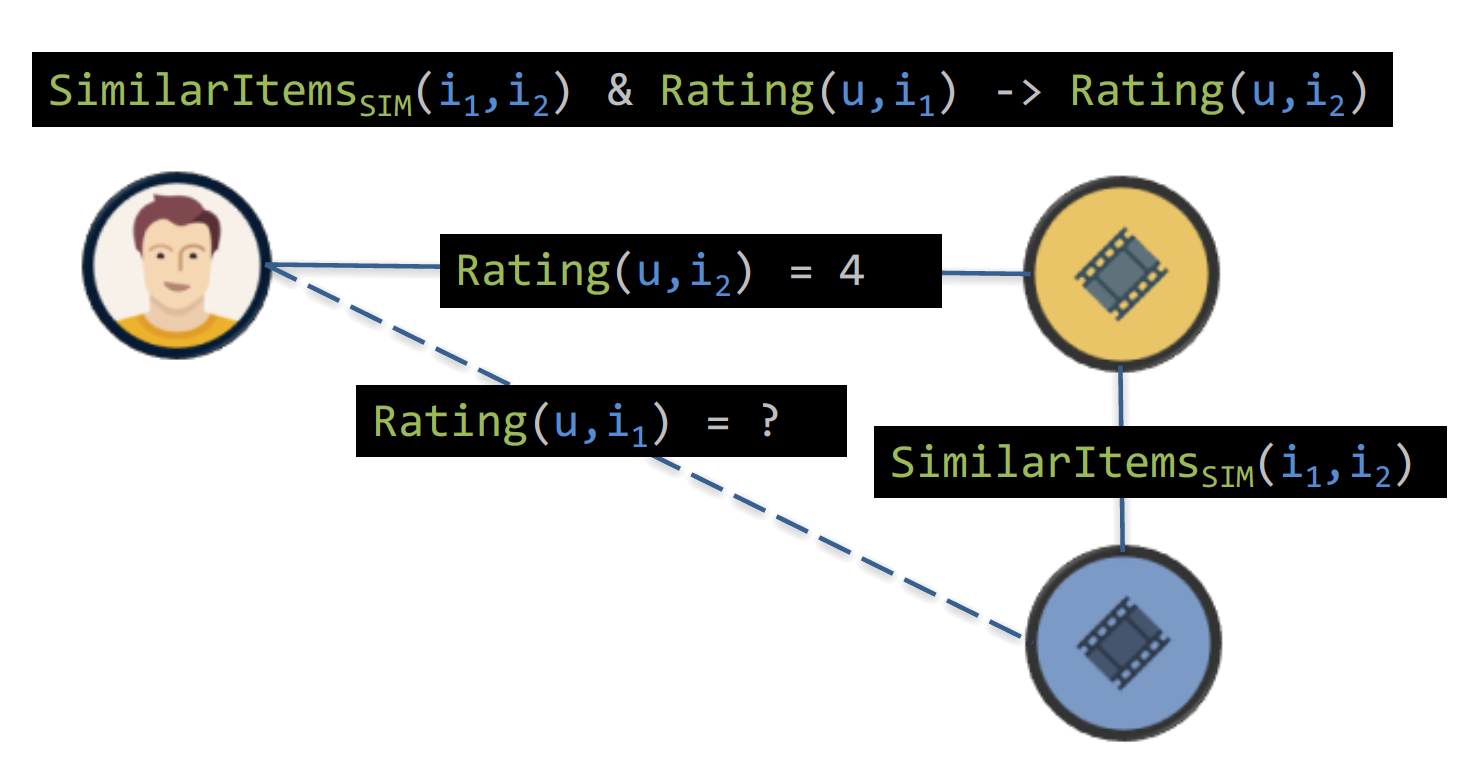
The rule states that IF items i1 and i2 are similar, for a given similarity measure, AND user u rated item i1 highly, THEN user u will rate item i2 highly. The predicate Rating(u, i) takes a value in the interval [0, 1] and represents the normalized value of the rating that a user u gave to an item i, while SimilarUserssim(u1, u2) is binary, with value 1 iff u1 is one of the k-nearest neighbors of u2. We note that we can use as many similarity metrics as we wish. Popular options include cosine, adjusted cosine, and Pearson correlation.
Working in a similar way we can introduce rules from the user-based neighborhood methods.
Intuitively, the rule states that IF users u1 and u2 are similar AND u1 rated i highly, then it is likely that u2 rated i highly as well. Like before, the predicate SimilarItemssim(i1, i2) is binary, with value 1 iff i1 is one of the k-nearest neighbors of i2 (using similarity measure SIM), while Rating(u, i) represents the normalized value of the rating of user u to item i, as discussed above. Again, we can use multiple similarity measures used in the literature for user similarities.
We continue by defining mean centering corrections that are usually used in the neighborhood-based methods. These corrections capture the fact that some items are very popular and that is why they get high ratings. Or they capture the fact that a user is strict so he rarely gives high ratings or the opposite. We introduce such corrections through the use of prior rules in our model.
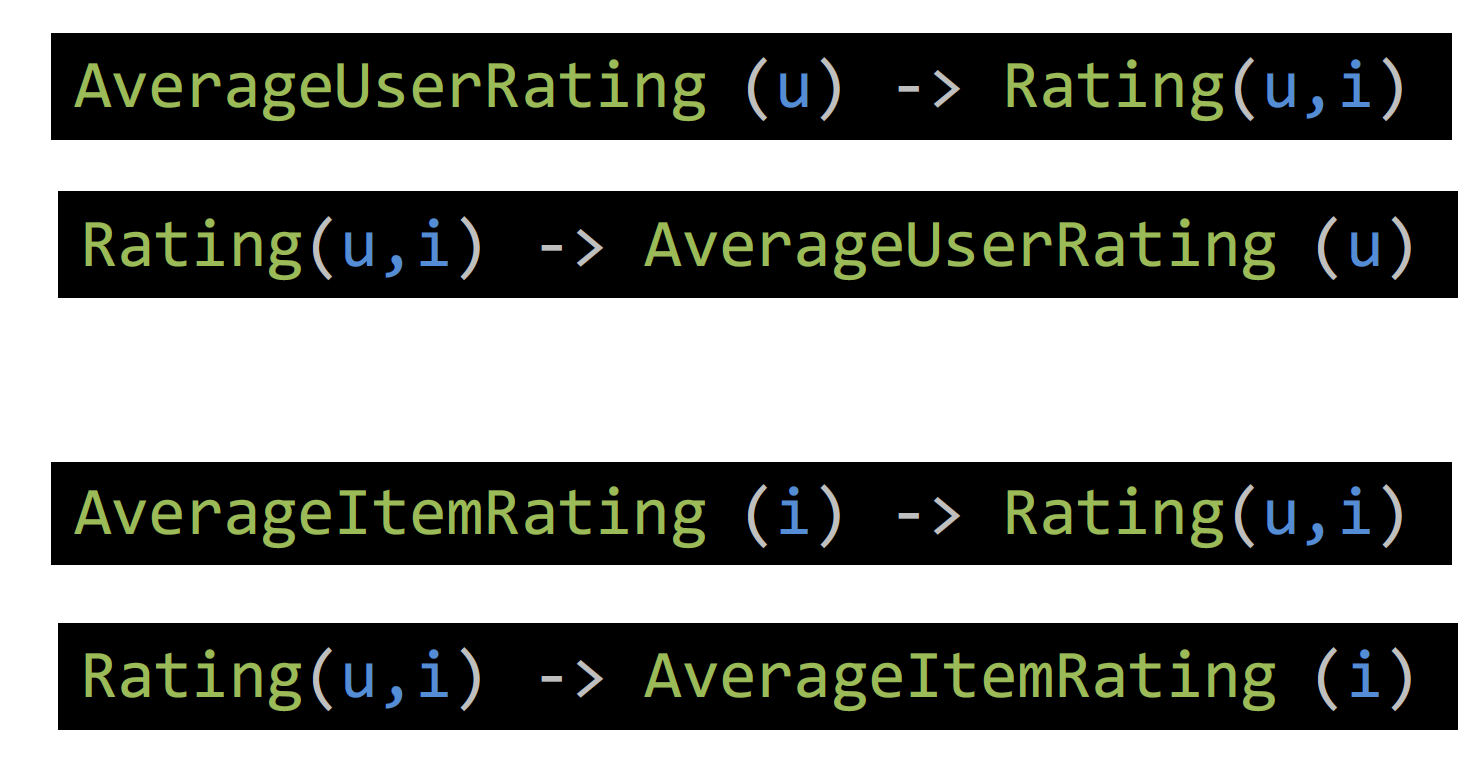
The first two rules state that the rating a user gives to an item should be close to the average rating of the user. The predicate AverageUserRating(u) represents the average of the ratings over the set of items that user u provided in the training set. The last two rules state the similar for the item case. Similarly, AverageUserRating(i) represents the average of the user ratings an item i has received. Each pair of PSL rules per-user and per-item corresponds to a “V-shaped” function centered at the average rating, which penalizes the predicted rating for being different in either direction from this average. These rules are also useful for the cold-start setting, where we might have no prior knowledge for a user or an item.
Additionally, we can incorporate rules that capture the relationships. Two users that are friends tend to give similar ratings.
Finally as we stated, we can use the predictions from other algorithms. We can do that by introducing rules in the form of priors, like the one shown below. We note that we can use as many different algorithms as we wish.
Finally, we note that HyPER is extensible beyond the rules and data types that I have shown here. If a new data source becomes available, the only thing that we need to do is to add another first-order PSL rule, and then retrain the model.
Code + Data: https://github.com/pkouki/recsys2015
References: [Bell et al.] R. Bell, Y. Koren, C. Volinsky, The BellKor Solution to the Netflix Prize, 2007